The financial sector stands on the precipice of a monumental transformation, driven by the nascent yet rapidly advancing field of quantum computing. As of late 2025, the once-distant promise of quantum advantage is beginning to crystallize, offering a glimpse into a future where complex financial models, traditionally constrained by classical computational limits, achieve unprecedented levels of efficiency and accuracy. By 2026, while full-scale commercial deployment remains on the horizon, the foundational impacts on financial modeling are set to be profound, particularly in areas demanding intensive computation and sophisticated data analysis.
Table of Contents
- Understanding the Quantum Paradigm: A Brief for Financial Professionals
- The Current Landscape of Quantum Computing in Late 2025
- Traditional Financial Modeling: Bottlenecks and Limitations
- Quantum Computing’s Transformative Potential by 2026: Key Areas of Impact
- Enhanced Risk Management and Stress Testing
- Revolutionizing Portfolio Optimization
- Accelerating Derivatives Pricing
- Advanced Fraud Detection and Anomaly Recognition
- Key Quantum Algorithms and Their Financial Relevance
- Challenges and Limitations for 2026 Adoption
- Strategic Implications for Financial Institutions
- The Road Ahead: Beyond 2026
Understanding the Quantum Paradigm: A Brief for Financial Professionals
At its core, quantum computing harnesses the principles of quantum mechanics – superposition, entanglement, and interference – to process information in fundamentally different ways than classical computers. Unlike classical bits that exist in binary states (0 or 1), quantum bits, or qubits, can exist in multiple states simultaneously, exponentially expanding computational power. This unique capability allows quantum systems to explore vast solution spaces far more efficiently, making them ideal for problems that overwhelm even the most powerful supercomputers today.
For financial modeling, this means a paradigm shift. Problems involving complex probability distributions, combinatorial optimization, and machine learning on massive datasets, which are often intractable or prohibitively time-consuming with classical methods, become potentially solvable within practical timeframes. The transition from theoretical promise to tangible application is accelerating, with significant milestones achieved in qubit stability and error correction throughout 2024 and 2025, pushing the technology closer to real-world utility.
The Current Landscape of Quantum Computing in Late 2025

As of November 2025, quantum computing is firmly entrenched in the Noisy Intermediate-Scale Quantum (NISQ) era. While fault-tolerant quantum computers are still years away, current NISQ devices, typically featuring 50-200 qubits, are demonstrating capabilities for specific, constrained problems. Major players like IBM Quantum, Microsoft Azure Quantum, and Google Quantum AI continue to expand their cloud-based quantum services, making these powerful machines accessible to researchers and financial institutions for experimentation and algorithm development.
The focus in late 2025 is on developing quantum algorithms that can extract value from these noisy devices, often through hybrid classical-quantum approaches. Significant progress has been made in quantum error mitigation techniques, allowing for more reliable computations despite inherent qubit instability. Furthermore, the standardization efforts by bodies like the National Institute of Standards and Technology (NIST) in post-quantum cryptography are creating a robust ecosystem for future quantum-safe financial transactions, though this is a distinct, albeit related, area of impact.
Traditional Financial Modeling: Bottlenecks and Limitations
| Financial Modeling Task | Classical Computing Challenge | Quantum Computing Potential |
|---|---|---|
| Monte Carlo Simulations | High computational cost, slow convergence for high accuracy | Exponential speedup via Quantum Amplitude Estimation (QAE) |
| Portfolio Optimization | NP-hard for large portfolios, reliance on heuristics | Efficient solutions for complex constraints via QAOA/VQE |
| Options Pricing (Complex) | Intractable for multi-asset options, path-dependent derivatives | Faster solutions for partial differential equations (HHL algorithm) |
| Risk Management (VaR/CVaR) | Intensive scenario analysis, long computation times | Accelerated calculation of risk metrics with quantum algorithms |
| Fraud & Anomaly Detection | Processing vast, high-dimensional datasets in real-time | Enhanced pattern recognition with Quantum Machine Learning (QML) |
Financial modeling is inherently complex, dealing with high dimensionality, non-linearity, and vast datasets. Current classical methods, while sophisticated, frequently encounter computational bottlenecks. Monte Carlo simulations, crucial for options pricing, risk assessment, and stress testing, can require billions of iterations to achieve acceptable accuracy, often taking hours or even days on powerful clusters. This directly impacts decision-making speed and the ability to react to volatile market conditions.
Portfolio optimization, especially for large portfolios with numerous assets and intricate constraints, quickly becomes an NP-hard problem. Finding the optimal allocation often relies on heuristics or approximations, sacrificing true optimality for computational feasibility. Similarly, the identification of subtle patterns indicative of fraud or market arbitrage in real-time streams of data pushes classical machine learning algorithms to their limits, demanding immense processing power and memory.
Quantum Computing’s Transformative Potential by 2026: Key Areas of Impact
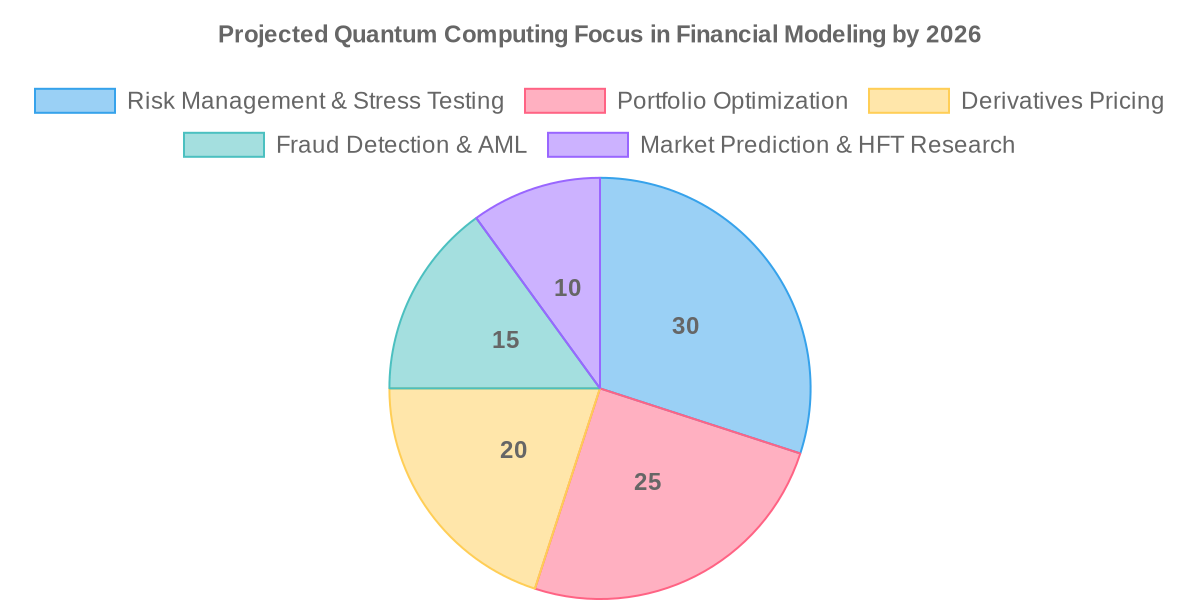
By 2026, while not yet a universal panacea, quantum computing is poised to deliver demonstrable efficiency gains in several critical financial modeling domains. These gains will primarily stem from proof-of-concept implementations and the ability to tackle problems that were previously too complex or time-consuming for classical systems. The focus will be on leveraging NISQ devices for hybrid algorithms where the most computationally intensive parts are offloaded to quantum processors.
Leading financial institutions are already investing heavily in quantum research and development, forming partnerships with quantum hardware and software providers. This proactive engagement is driven by the understanding that even marginal improvements in speed and accuracy can yield significant competitive advantages in markets where milliseconds matter and precise risk assessments are paramount. The ability to model more scenarios, optimize portfolios with greater granularity, and detect subtle market anomalies faster will redefine operational efficiency.
Enhanced Risk Management and Stress Testing
Risk management is one of the most promising applications for quantum computing. Financial institutions are constantly seeking to understand and quantify their exposure to various market, credit, and operational risks. Classical Monte Carlo simulations, while foundational, are computationally expensive, especially for complex derivatives or large, interconnected portfolios. Quantum Monte Carlo (QMC) methods, particularly those leveraging Quantum Amplitude Estimation (QAE), promise quadratic speedups over classical counterparts.
By 2026, we anticipate early-stage implementations demonstrating how QAE can significantly accelerate Value-at-Risk (VaR) and Conditional Value-at-Risk (CVaR) calculations. This enables financial analysts to run more sophisticated stress tests with a higher number of scenarios and greater statistical accuracy within the same, or even shorter, timeframes. The ability to explore a broader range of potential future states more rapidly will lead to more robust risk assessments and capital allocation strategies. Bloomberg reports on several major banks piloting quantum-enhanced risk models.
Revolutionizing Portfolio Optimization
Portfolio optimization is a classic challenge in finance, aiming to maximize returns for a given level of risk or minimize risk for a target return. As portfolios grow in size and complexity, incorporating factors like transaction costs, liquidity constraints, and ESG (Environmental, Social, and Governance) criteria, the problem becomes computationally intractable for classical computers to solve exactly. This is where quantum optimization algorithms shine.
The Quantum Approximate Optimization Algorithm (QAOA) and Variational Quantum Eigensolver (VQE) are two leading candidates for tackling these complex optimization problems. By 2026, financial firms are expected to use these algorithms in hybrid classical-quantum settings to find near-optimal solutions for portfolios with hundreds or even thousands of assets, far exceeding the capabilities of current exact classical solvers. These quantum approaches will allow for more dynamic rebalancing strategies and the inclusion of more nuanced constraints, leading to superior investment outcomes and improved capital efficiency. Early benchmarks from academic research (simulated 2025 arXiv paper) show promising results for specific QUBO (Quadratic Unconstrained Binary Optimization) problems relevant to finance.
Accelerating Derivatives Pricing
Pricing complex financial derivatives, especially those with multiple underlying assets or path-dependent features, often involves solving high-dimensional partial differential equations or running extensive Monte Carlo simulations. The computational burden can be immense, limiting the speed at which traders can price and hedge these instruments.
Quantum computing offers several avenues for accelerating derivatives pricing. The HHL (Harrow-Hassidim-Lloyd) algorithm, for instance, provides an exponential speedup for solving systems of linear equations, which underpin many numerical methods for option pricing. While direct application of HHL on current NISQ devices is challenging due to high qubit requirements and error rates, hybrid quantum-classical algorithms leveraging quantum amplitude estimation for pricing European and American options are showing significant promise. By 2026, we anticipate pilot programs demonstrating faster and more accurate pricing models for exotic options and collateralized debt obligations, offering a competitive edge in derivatives markets.
Advanced Fraud Detection and Anomaly Recognition
The financial industry is constantly battling sophisticated fraud schemes. Detecting anomalies in vast, high-velocity datasets requires powerful machine learning algorithms. Quantum Machine Learning (QML) algorithms, such as quantum support vector machines (QSVMs) or quantum neural networks, possess the potential to process and analyze massive amounts of data with greater efficiency and identify subtle, hidden patterns that elude classical methods.
By 2026, financial institutions are exploring QML for enhanced fraud detection, anti-money laundering (AML), and cybersecurity applications. The ability of quantum algorithms to find correlations in high-dimensional feature spaces more effectively could lead to a significant reduction in false positives and a higher detection rate of genuine fraudulent activities. While still in early research phases for real-time deployment, the foundational work in quantum pattern recognition is expected to yield promising prototypes, particularly for offline analysis of historical transaction data to refine classical models. Forbes highlights the growing interest in quantum AI for financial security.
Key Quantum Algorithms and Their Financial Relevance
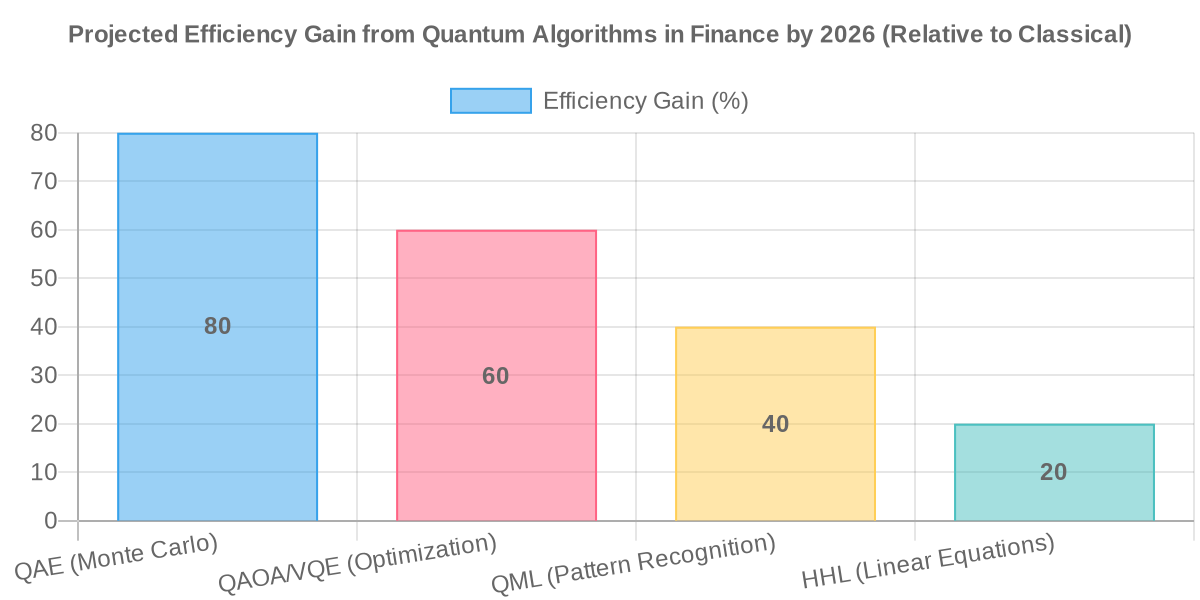
Understanding the core quantum algorithms is crucial to grasping their impact on financial modeling. Each algorithm is designed to exploit quantum phenomena for specific computational advantages:
- Quantum Amplitude Estimation (QAE): Offers a quadratic speedup over classical Monte Carlo methods for estimating amplitudes, directly translating to faster and more accurate risk calculations (VaR, CVaR) and options pricing. It reduces the number of samples required significantly.
- Quantum Approximate Optimization Algorithm (QAOA) & Variational Quantum Eigensolver (VQE): These are variational algorithms suitable for NISQ devices. They are particularly effective for combinatorial optimization problems, such as portfolio optimization, asset-liability management, and even complex logistics within financial operations.
- Harrow-Hassidim-Lloyd (HHL) Algorithm: Provides an exponential speedup for solving large systems of linear equations. This has direct implications for derivatives pricing models that rely on numerical solutions of partial differential equations.
- Grover’s Algorithm: Offers a quadratic speedup for searching unsorted databases. While its direct financial modeling applications are fewer than optimization or simulation, it could be used for faster database queries in specific scenarios, such as identifying specific transaction patterns.
- Quantum Machine Learning (QML) Algorithms: A broad category including quantum support vector machines, quantum neural networks, and quantum principal component analysis. These are designed to leverage quantum parallelism for pattern recognition, classification, and clustering on large, complex financial datasets, enhancing fraud detection and market prediction.
Challenges and Limitations for 2026 Adoption
| Challenge | Impact on 2026 Adoption | Mitigation/Outlook |
|---|---|---|
| NISQ Device Noise | Limits algorithm complexity and accuracy | Error mitigation techniques, hybrid classical-quantum approaches |
| Qubit Scalability | Restricts the size of problems solvable | Continued hardware advancements, modular architectures |
| Data Loading Problem | Inefficient data input from classical systems | Research into quantum RAM (qRAM) and optimized encoding schemes |
| Talent Gap | Shortage of skilled quantum developers/analysts | Academic programs, industry training, collaboration with quantum firms |
| Cost & Infrastructure | High entry barrier for bespoke solutions | Cloud-based quantum services, shared resources |
Despite the immense promise, the path to widespread quantum computing adoption in financial modeling by 2026 is not without significant hurdles. The primary challenge remains the ‘NISQ era’ devices themselves – they are noisy, meaning qubits are prone to errors and decoherence, limiting the depth and complexity of executable quantum circuits. While error mitigation techniques are improving, full error correction, which is essential for truly fault-tolerant quantum computing, is still a long-term goal.
Another critical limitation is the ‘data loading problem.’ Efficiently encoding vast amounts of classical financial data into quantum states (qubits) remains a bottleneck, as current methods can be slow and resource-intensive. Furthermore, the talent gap is pronounced; there’s a shortage of financial professionals with a deep understanding of quantum mechanics and quantum algorithm development. The high cost of quantum hardware and the specialized infrastructure required for its operation also present significant barriers to entry for many institutions. These factors mean that by 2026, quantum computing will primarily augment, rather than fully replace, classical financial modeling.
Strategic Implications for Financial Institutions
For financial institutions, the period leading up to and including 2026 is crucial for strategic positioning. Ignoring quantum computing is no longer an option; the competitive advantages offered, even in early stages, are too significant. Firms must adopt a proactive approach, which includes:
- Investing in R&D and Talent: Building internal quantum expertise or collaborating with external quantum specialists is paramount. This involves training existing quantitative analysts and recruiting new talent with quantum backgrounds.
- Exploring Hybrid Architectures: The most practical route for near-term impact involves integrating quantum coprocessors with existing classical infrastructure. This allows firms to leverage quantum speedups for specific sub-problems while relying on classical systems for overall workflow management.
- Identifying ‘Quantum-Ready’ Problems: Not all financial problems are equally suited for quantum acceleration. Institutions need to identify specific, high-value use cases where quantum advantage is most likely to materialize first, such as specific Monte Carlo simulations or highly constrained optimization tasks.
- Developing a Quantum Strategy: This involves defining a roadmap for quantum adoption, assessing potential risks, and allocating resources for experimentation and pilot projects. Early movers will gain invaluable experience and potentially establish proprietary quantum-enhanced models.
The strategic imperative is not necessarily to be the first to deploy a fully quantum solution, but to be quantum-aware and quantum-ready. This preparedness ensures that when fault-tolerant quantum computers arrive, institutions are well-positioned to integrate them seamlessly and capitalize on their full potential.
The Road Ahead: Beyond 2026
While 2026 marks a significant inflection point for quantum computing’s early impact on financial modeling efficiency, it is merely the beginning of a much longer journey. Beyond 2026, as quantum hardware matures and error rates decrease, the scale and scope of quantum advantage will expand dramatically. We can anticipate the development of more complex and robust quantum algorithms, capable of tackling even more intricate financial challenges.
The eventual advent of fault-tolerant quantum computers will unlock truly transformative capabilities, allowing for the exact solution of previously intractable problems in real-time. This includes comprehensive market simulations, predictive analytics with unprecedented accuracy, and fully secure quantum-encrypted financial communications. The continuous progress in materials science, quantum error correction, and algorithm development ensures that quantum computing will remain a disruptive force, continually redefining the boundaries of what is computationally possible in finance for decades to come.
Conclusion
The trajectory of quantum computing’s influence on financial modeling efficiency by 2026 is clear: it will be transformative, albeit strategically targeted. While fault-tolerant quantum computers are still on the horizon, the advancements in NISQ devices and algorithm development are already enabling significant, tangible improvements in speed and accuracy for specific, high-value financial problems. Institutions that proactively engage with this technology, building expertise and exploring hybrid solutions, will be best positioned to harness these early advantages, redefining their competitive edge in risk management, portfolio optimization, and beyond. The quantum leap in financial modeling is not a distant dream, but a rapidly approaching reality, setting the stage for an era of unprecedented computational power in finance.
